퍼셉트론 perceptron

퍼셉트론이란?

신경망과 딥러닝의 기원이 되는 퍼셉트론은 1957년 프랑크 로젠블라트가 고안한 알고리즘이다. 

퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력한다.

실제 전류와 달리 퍼셉트론 신호는 '흐른다와 안흐른다(1 or 0)'의 두가지 값을 가진다.

 

입력이 2개인 퍼셉트론

 

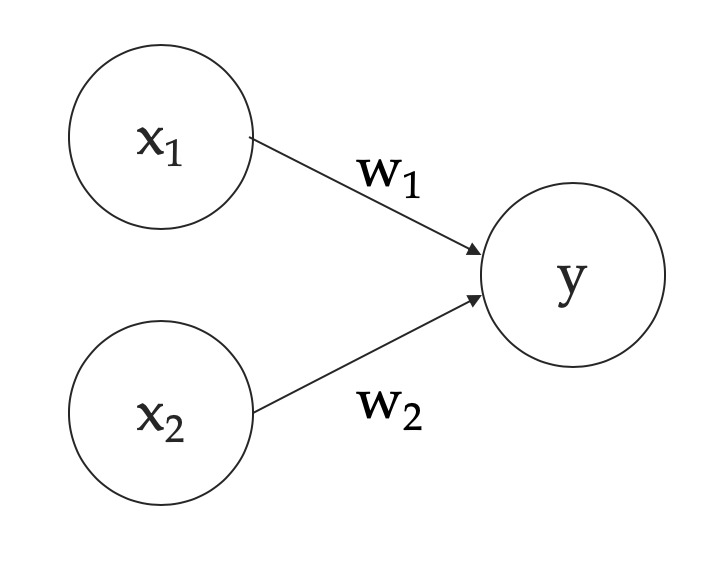
• 입력 신호 : x1, x2 - 입력 신호가 있는 층을 입력층(Input layer)이라 한다.
• 출력 신호 : y
• 가중치 (weight) : w1, w2
• 원 : 뉴런, 노드, 유닛이라 불린다.
• 선 (edge) : 선은 데이터의 흐름(flow)을 나타내는 길 (tensor로 이 흐름을 구현하므로 텐서플로이다.)

 

 

퍼셉트론 동작 원리

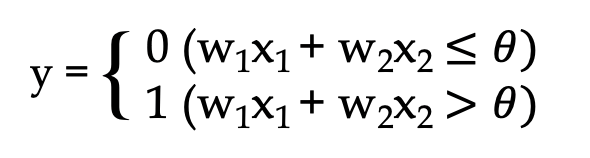
입력 신호가 뉴런에 보내질 때 각각 고유한 가중치가 곱해진다.

뉴런에서 보내온 신호의 총합이 정해진 한계(임계값 θ)를 넘어설 때만 1을 출력한다.

 

단순한 논리 회로

(w1, w2, θ)가 (0.5, 0.5, 0.7)일 때 퍼셉트론 AND 게이트를 충족하는 이유는? 

• AND 게이트

x1	x2	y
0	0	0
1	0	0
0	1	0
1	1	1

 

x1	x2		y
0*0.5=0	0*0.5=0	0+0 > 0.7	0
1*0.5=0.5	0*0.5=0	0.5+0 > 0.7	0
0*0.5=0	1*0.5=0.5	0 + 0.5 > 0.7	0
1*0.5=0.5	1*0.5=0.5	0.5 + 0.5 > 0.7	1

 

 

가중치와 편향 

    

θ를 -b로 치환하면 퍼셉트론의 동작이 다음과 같이 바뀐다. 여기서 b를 편향(bias)라 한다.

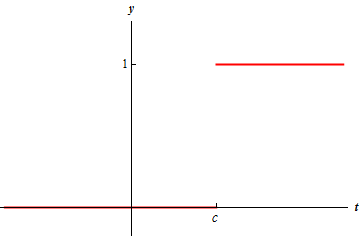
퍼셉트론은 입력 신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력한다.

-> 계단함수(step function)라 부른다.

 

 

http://tutorial.math.lamar.edu/Classes/DE/StepFunctions.aspx

 

 

 

퍼셉트론의 한계

AND와 OR 게이트와 달리 XOR 게이트를 만족하는 매개변수 값은 구할 수 없다. 

퍼셉트론은 직선 하나로 나눈 영역만 표혈할 수 있다는 한계를 가지기 때문이다.

 

• XOR 게이트

AND, NAND, OR 게이트를 조합해 구현한 XOR 게이트는 다음과 같다.

출처: www.slideshare.net/ssuser892bc4 

 

• XOR 게이트의 진리표

x1	x2	s1  NAND	s2 OR	y AND
0	0	1	0	0
1	0	1	1	1
0	1	1	1	1
1	1	0	1	0

 

따라서 단층 퍼셉트론으로는 표현하지 못한 것을 층을 하나 늘려 구현할 수 있다. 

퍼셉트론은 층을 쌓아 (깊게 하여) 더 다양한 것을 표현할 수 있다.

-> 다층 퍼셉트론 (multi-layer perceptron), 신경망의 등장